
Expected Value and Variance

Substitution and Income Effects
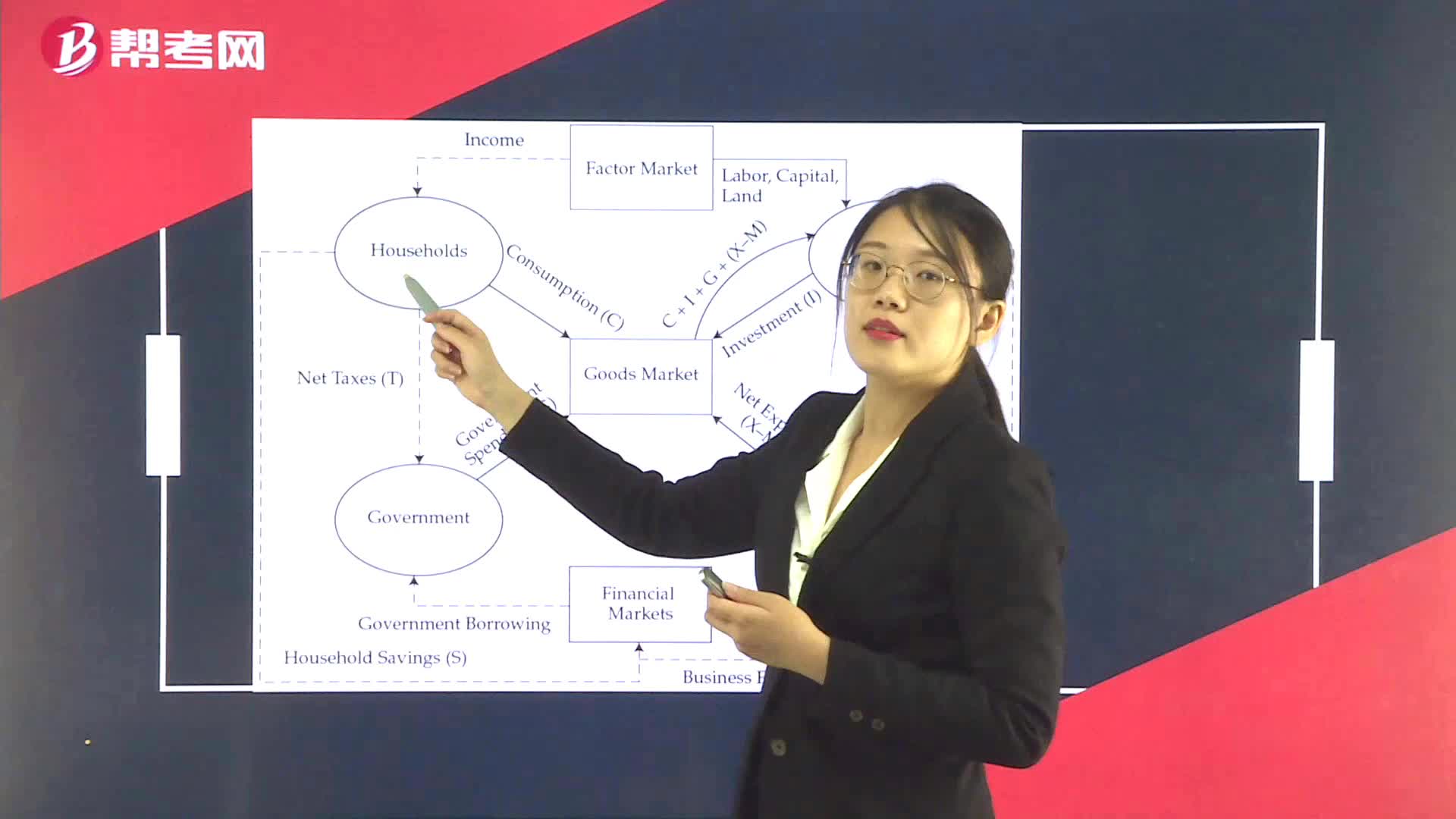
Output, Income, and Expenditure Flows

Imports and Exports

GDP and GNP

Hypothesis Tests Concerning Variance
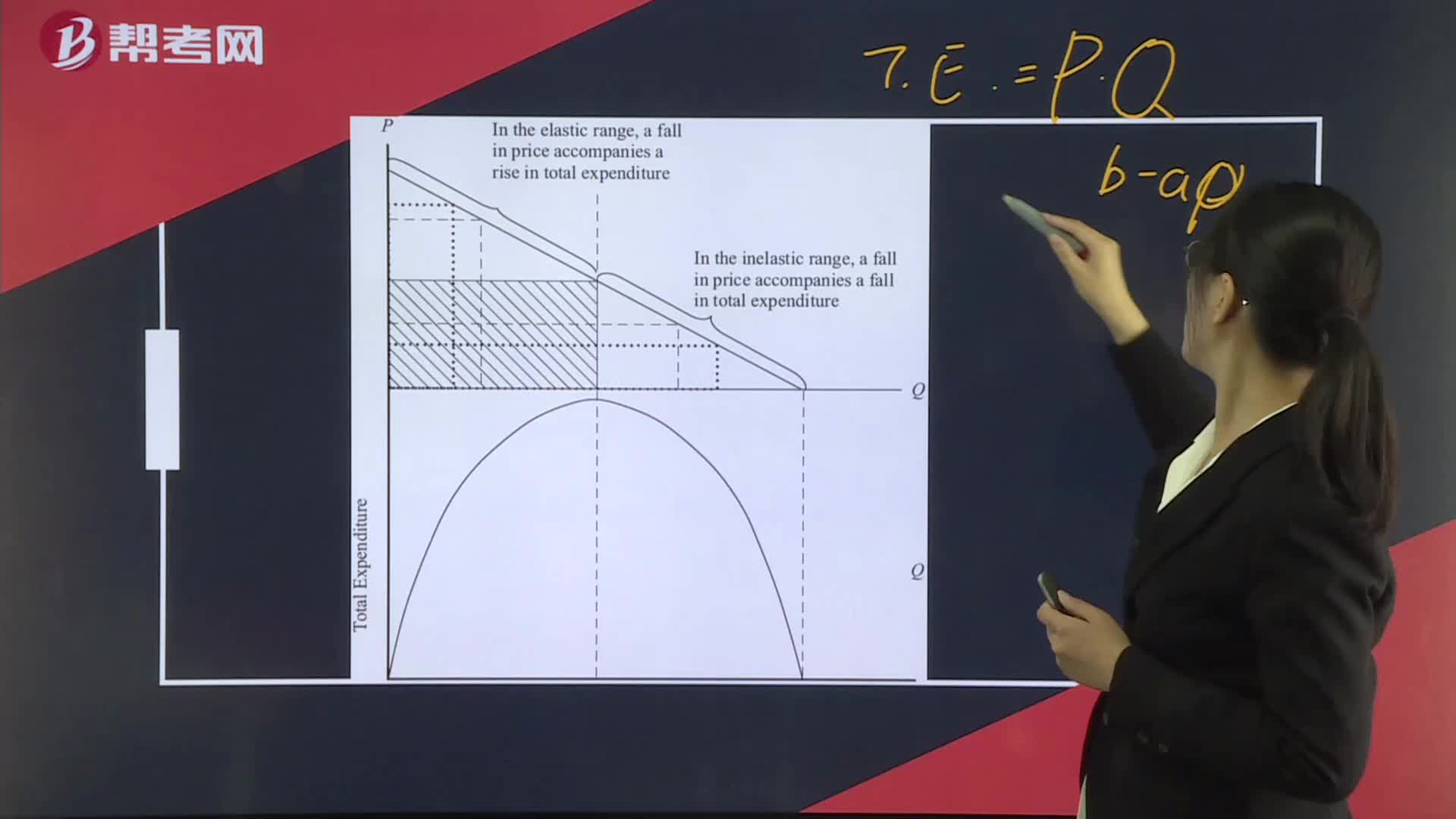
Elasticity and Total Expenditure

Absolute and Comparative Advantage

Economic Profit and Accounting Profit

Shifts in the AD and AS curves and Equilibriums

Financial Statements and Supplementary Information

Financial Notes and Supplementary Schedules

下載億題庫APP
聯(lián)系電話:400-660-1360













